Usage
Usage
You’ll use the Coveo Quantic library to assemble Lightning Web Components (LWCs) which are managed in Salesforce Developer Experience (DX) projects using the Salesforce CLI.
This article provides an overview of how to use Quantic by guiding you through the implementation of a search interface LWC.
Prerequisites
-
You’ve installed the Salesforce CLI, with Dev Hub enabled in your Salesforce organization.
-
Although it’s not necessary, we recommend that you install and configure Coveo for Salesforce v4 or a later package. It can automatically take care of important steps at the search token authentication stage.
Install Quantic
Quantic is released as an unlocked package. You can install it using the following links:
You can also install Quantic with the Salesforce CLI package install command:
sf package install --package 04t6g000008b6ErAAI --target-org <USER_NAME>where you replace <USER_NAME> with your username in the target Salesforce organization.
|
|
Note
You should always keep your Apex code clean and compiled.
However, if you only want to compile the package Apex code during the installation, use the |
Create a Salesforce DX project
You need a Salesforce DX project to manage your LWCs.
You can create one with the project generate command:
sf project generate --name MyProjectOnce you’ve created your project, you have to indicate to your Salesforce organization that you’ll be using the Quantic library.
Open the sfdx-project.json file at the root of your project folder and add the following dependency to the packageDirectories object:
{
"package": "quantic",
"versionNumber": "3.2.5.NEXT",
"path": "force-app/quantic/",
"default": false,
"dependencies": [
{
"package": "Quantic",
"versionNumber": "3.2.5.LATEST"
}
]
}Make sure that you use version numbers which match the version of Quantic that’s installed in your Salesforce organization. You can check which one you have with the Installed Packages tool in your Salesforce organization’s Setup menu.
If you want to update to the latest version of Quantic in your Salesforce organization, repeat the installation process with the newest package identifier.
Assemble your component
You can use Quantic by creating LWCs that assemble the target Quantic components.
Because Quantic is released as an unlocked package, its components will be available under the default namespace c.
|
|
You can find a complete example of a search interface LWC in the Quantic project repository. |
Setup
The structure of your Salesforce DX project is largely up to you. However, you may want to retrieve Quantic locally so that you can navigate to the existing Quantic components and use them as examples when building your LWC.
Retrieve Quantic
You can import the Quantic project into yours with the project retrieve start command:
sf project retrieve start --package-name Quantic --target-metadata-dir ./ --target-org <USER_NAME>where you replace <USER_NAME> with your username in the target Salesforce organization.
Once you’ve downloaded the file, unzip it and move its contents to force-app/quantic.
Create your LWC
Create your LWC (for example, mySearchPage) with the lightning generate component command:
sf lightning generate component --name mySearchPage --type lwcThe structure of your new LWC should look like the following:
mySearchPage/ ├── mySearchPage.html ├── mySearchPage.js ├── mySearchPage.js-meta.xml
HTML
This is where you assemble HTML elements and leverage Quantic components to build your search interface LWC.
<template>
<div onregisterresulttemplates={handleResultTemplateRegistration}>  <div class="search__grid">
<c-quantic-search-interface engine-id={engineId} search-hub={searchHub}>
<div class="search__grid">
<c-quantic-search-interface engine-id={engineId} search-hub={searchHub}>  <div class="slds-grid slds-grid_vertical slds-grid_align-center">
<div class="slds-grid slds-grid_vertical slds-grid_align-center">  <div class="slds-col slds-size_1-of-1 slds-large-size_6-of-12 slds-align-middle">
<div class="slds-m-vertical_small">
<c-quantic-search-box engine-id={engineId}></c-quantic-search-box>
</div>
</div>
<div class="slds-col">
<div class="slds-grid slds-gutters_direct slds-wrap main slds-grid_align-center">
<div class="slds-col slds-size_1-of-1 slds-large-size_6-of-12 slds-align-middle">
<div class="slds-m-vertical_small">
<c-quantic-search-box engine-id={engineId}></c-quantic-search-box>
</div>
</div>
<div class="slds-col">
<div class="slds-grid slds-gutters_direct slds-wrap main slds-grid_align-center">  <div class="slds-col slds-order_2 slds-large-order_1 slds-size_1-of-1 slds-large-size_3-of-12">
<div class="slds-m-bottom_large">
<c-quantic-facet field="objecttype" label="Type" engine-id={engineId}></c-quantic-facet>
</div>
<div class="slds-m-bottom_large">
<c-quantic-facet display-values-as="link" field="filetype" label="File Type" engine-id={engineId}></c-quantic-facet>
</div>
</div>
<div class="slds-col slds-order_1 slds-large-order_2 slds-size_1-of-1 slds-large-size_6-of-12">
<ul class="slds-tabs_default slds-tabs_default__nav" role="tablist">
<c-quantic-tab label="All" engine-id={engineId}></c-quantic-tab>
<c-quantic-tab label="Articles" expression="@sfkbid" engine-id={engineId}></c-quantic-tab>
</ul>
<c-quantic-result-list engine-id={engineId}></c-quantic-result-list>
<div class="slds-col slds-order_2 slds-large-order_1 slds-size_1-of-1 slds-large-size_3-of-12">
<div class="slds-m-bottom_large">
<c-quantic-facet field="objecttype" label="Type" engine-id={engineId}></c-quantic-facet>
</div>
<div class="slds-m-bottom_large">
<c-quantic-facet display-values-as="link" field="filetype" label="File Type" engine-id={engineId}></c-quantic-facet>
</div>
</div>
<div class="slds-col slds-order_1 slds-large-order_2 slds-size_1-of-1 slds-large-size_6-of-12">
<ul class="slds-tabs_default slds-tabs_default__nav" role="tablist">
<c-quantic-tab label="All" engine-id={engineId}></c-quantic-tab>
<c-quantic-tab label="Articles" expression="@sfkbid" engine-id={engineId}></c-quantic-tab>
</ul>
<c-quantic-result-list engine-id={engineId}></c-quantic-result-list>  <div class="slds-var-m-vertical_medium">
<c-quantic-pager engine-id={engineId}></c-quantic-pager>
</div>
</div>
</div>
</div>
</div>
</c-quantic-search-interface>
</div>
</div>
</template>
<div class="slds-var-m-vertical_medium">
<c-quantic-pager engine-id={engineId}></c-quantic-pager>
</div>
</div>
</div>
</div>
</div>
</c-quantic-search-interface>
</div>
</div>
</template>Attach the handleResultTemplateRegistration function on the event thrown to register result templates. |
|
Use the QuanticSearchInterface component and set its engine-id and search-hub properties, as well as any others that you require.
In this example, these properties are set with variables whose default values are defined in the XML configuration file, but you can also set specific values here, such as search-hub="example-search-hub".
Typically, you’ll set the actual values for the properties that you expose through the XML file in the Salesforce Experience Builder.
This search interface component is required to handle the Headless search engine and localization configurations.
Most Quantic components require an |
|
| Out of the box, Quantic lets you use Salesforce Lightning Design System (SLDS) styling classes. In this case, you’re using the Grid utility. | |
Use the SLDS gutters_direct class, which only applies to direct children.
The gutters class can cause styling issues with certain Quantic child components. |
|
Your result templates will initialize inside the QuanticResultList component. |
|
|
You can find a more detailed example in the Quantic project repository. |
XML
The XML configuration file is where you define the targets of your LWC. You also specify the parameters whose values are requested through the Salesforce Experience Builder and can set their default values. These take precedence over the values you set in your LWC JavaScript file.
<?xml version="1.0" encoding="UTF-8"?>
<LightningComponentBundle xmlns="http://soap.sforce.com/2006/04/metadata">
<apiVersion>56.0</apiVersion>
<isExposed>true</isExposed>
<targets>  <target>lightning__RecordPage</target>
<target>lightning__AppPage</target>
<target>lightning__HomePage</target>
<target>lightningCommunity__Page</target>
<target>lightningCommunity__Default</target>
</targets>
<targetConfigs>
<targetConfig targets="lightningCommunity__Default">
<target>lightning__RecordPage</target>
<target>lightning__AppPage</target>
<target>lightning__HomePage</target>
<target>lightningCommunity__Page</target>
<target>lightningCommunity__Default</target>
</targets>
<targetConfigs>
<targetConfig targets="lightningCommunity__Default">  <property name="engineId" type="String" default="example-search-community" label="Enter Coveo Headless engine ID"/>
<property name="searchHub" type="String" default="example-search-hub-community" label="Enter Search Hub"/>
</targetConfig>
<targetConfig targets="lightning__AppPage, lightning__RecordPage, lightning__HomePage">
<property name="engineId" type="String" default="example-search" label="Enter Coveo Headless engine ID"/>
<property name="searchHub" type="String" default="example-search-hub" label="Enter Search Hub"/>
</targetConfig>
</targetConfigs>
</LightningComponentBundle>
<property name="engineId" type="String" default="example-search-community" label="Enter Coveo Headless engine ID"/>
<property name="searchHub" type="String" default="example-search-hub-community" label="Enter Search Hub"/>
</targetConfig>
<targetConfig targets="lightning__AppPage, lightning__RecordPage, lightning__HomePage">
<property name="engineId" type="String" default="example-search" label="Enter Coveo Headless engine ID"/>
<property name="searchHub" type="String" default="example-search-hub" label="Enter Search Hub"/>
</targetConfig>
</targetConfigs>
</LightningComponentBundle>| The targets in which your LWC will be available. | |
| Expose the properties that you want to be able to edit in the Salesforce Experience Builder. You can set different values for each target. You passed these variables to instantiate Quantic components in your HTML file. |
|
|
You can find a more detailed example in the Quantic project repository. |
Result templates
Result templates are HTML files that determine the format of the individual result items in a search interface.
You build them by assembling SLDS elements and Quantic components.
Inside these, you can invoke the result variable, which is passed by the result template manager and holds various result item attributes.
Typically, you’ll want to define your result templates in a folder which is a sibling of your other search interface files. You’ll connect them using conditions in your JavaScript file.
mySearchPage/ ├── resultTemplates/ │ ├── youtubeResultTemplate.html ├── mySearchPage.html ├── mySearchPage.js ├── mySearchPage.js-meta.xml
While optional, we recommend using the QuanticResultTemplate component.
This component makes it easier to create responsive and stylistically cohesive templates by providing a recommended display structure that uses predefined and formatted LWC slots.
<template>
<c-quantic-result-template>  <c-quantic-result-label slot="label" result={result}></c-quantic-result-label>
<c-quantic-result-label slot="label" result={result}></c-quantic-result-label>  <div slot="badges" class="slds-grid slds-grid_vertical-align-center">
<div class="slds-m-right_xx-small">
<c-quantic-result-tag variant="recommended" result={result}></c-quantic-result-tag>
</div>
<c-quantic-result-tag variant="featured" result={result}></c-quantic-result-tag>
</div>
<template if:true={resultHasPreview}>
<c-quantic-result-quickview slot="actions" engine-id={engineId} result={result}></c-quantic-result-quickview>
</template>
<p slot="date" class="slds-size_xx-small">
<lightning-formatted-date-time value={result.raw.date}></lightning-formatted-date-time>
<div slot="badges" class="slds-grid slds-grid_vertical-align-center">
<div class="slds-m-right_xx-small">
<c-quantic-result-tag variant="recommended" result={result}></c-quantic-result-tag>
</div>
<c-quantic-result-tag variant="featured" result={result}></c-quantic-result-tag>
</div>
<template if:true={resultHasPreview}>
<c-quantic-result-quickview slot="actions" engine-id={engineId} result={result}></c-quantic-result-quickview>
</template>
<p slot="date" class="slds-size_xx-small">
<lightning-formatted-date-time value={result.raw.date}></lightning-formatted-date-time>  </p>
<h3 slot="title" class="slds-truncate">
<c-quantic-result-link result={result} engine-id={engineId}></c-quantic-result-link>
</h3>
<div slot="visual" class="slds-size_1-of-1 slds-medium-size_1-of-4 slds-large-size_1-of-4 slds-p-right_x-small slds-m-top_xx-small slds-m-bottom_x-small">
<img style="border-radius: 4px; border: none;" src={videoThumbnail}></img>
</p>
<h3 slot="title" class="slds-truncate">
<c-quantic-result-link result={result} engine-id={engineId}></c-quantic-result-link>
</h3>
<div slot="visual" class="slds-size_1-of-1 slds-medium-size_1-of-4 slds-large-size_1-of-4 slds-p-right_x-small slds-m-top_xx-small slds-m-bottom_x-small">
<img style="border-radius: 4px; border: none;" src={videoThumbnail}></img>  </div>
<div slot="excerpt">
{result.Excerpt}
</div>
<div slot="bottom-metadata" class="slds-grid slds-text-align_left slds-m-top_xx-small" style="font-size: 10px">
<lightning-icon icon-name="utility:clock" size="xx-small"></lightning-icon>
<span class="slds-m-left_xxx-small">{videoTimeSpan}</span>
</div>
</c-quantic-result-template>
</template>
</div>
<div slot="excerpt">
{result.Excerpt}
</div>
<div slot="bottom-metadata" class="slds-grid slds-text-align_left slds-m-top_xx-small" style="font-size: 10px">
<lightning-icon icon-name="utility:clock" size="xx-small"></lightning-icon>
<span class="slds-m-left_xxx-small">{videoTimeSpan}</span>
</div>
</c-quantic-result-template>
</template>Wrap your template in the QuanticResultTemplate component. |
|
Use the QuanticResultLabel component with the label slot.
To instantiate this component, you don’t need to specify the engine ID, but you do need to pass the result item. |
|
In the date slot, pass the result’s raw.date field to the Lightning Formatted Date Time component. |
|
The QuanticResult component exposes a videoThumbnail attribute which you can use to display the video thumbnail. |
|
|
You can find more result template examples in the Quantic project repository. |
JavaScript
This is where you connect your result templates with your main HTML file using conditions. It’s also where you define the variables that you used in the HTML file, whose values you set in the XML file.
import youtubeTemplate from './resultTemplates/youtubeResultTemplate.html';
import {LightningElement, api} from 'lwc';
export default class MySearchPage extends LightningElement {
@api engineId = 'example-search';  @api searchHub = 'example-search-hub';
handleResultTemplateRegistration(event) {
@api searchHub = 'example-search-hub';
handleResultTemplateRegistration(event) {  event.stopPropagation();
event.stopPropagation();  const resultTemplatesManager = event.detail;
const resultTemplatesManager = event.detail;  const isYouTube = CoveoHeadless.ResultTemplatesHelpers.fieldMustMatch(
const isYouTube = CoveoHeadless.ResultTemplatesHelpers.fieldMustMatch(  'filetype',
['YouTubeVideo']
);
resultTemplatesManager.registerTemplates(
'filetype',
['YouTubeVideo']
);
resultTemplatesManager.registerTemplates(  {
content: youtubeTemplate,
{
content: youtubeTemplate,  conditions: [isYouTube],
fields: ['ytvideoid', 'ytvideoduration'],
conditions: [isYouTube],
fields: ['ytvideoid', 'ytvideoduration'],  priority: 1
priority: 1  },
);
};
}
},
);
};
}| Define the variables that you used in the HTML file and set their default values. The values that you set here are secondary to the ones that you set in your XML file. | |
The function that you attached to the onregisterresulttemplates event in your HTML file.
As its name suggests, it lets you register your result templates. |
|
| Since you caught the event, stop its propagation. | |
The detail property contains a result template manager, which you’ll store in a variable. |
|
| Create a condition that matches YouTube videos. | |
| Register the result template on the result template manager. | |
This line and the next make your youtubeTemplate only apply to result items that fulfill the isYoutube condition.
If a result item doesn’t match the conditions of any of your result templates, then the default Quantic one applies. |
|
Specify the fields to include in the search requests made by Quantic, because you need them in your youtubeTemplate.
By default, the Coveo index doesn’t return all possible item field values, so you must specify any non-default fields that you want to use in your result templates. |
|
| Sets the priority of the result template. If the conditions of multiple templates are satisfied by a given result, the template with the highest priority is selected. If multiple templates have equal priority, the first template registered is selected. |
|
|
You can find a more detailed example in the Quantic project repository. |
CSS
You can use SLDS styling classes in your LWC markup.
You can also add a .css file at the root of your project folder for further styling.
.search__grid {
position: relative;
padding: 12px;
background: #fff;
border-radius: .25rem;
background-clip: padding-box;
}Search token provider
If you were to deploy your LWC now, it would return results.
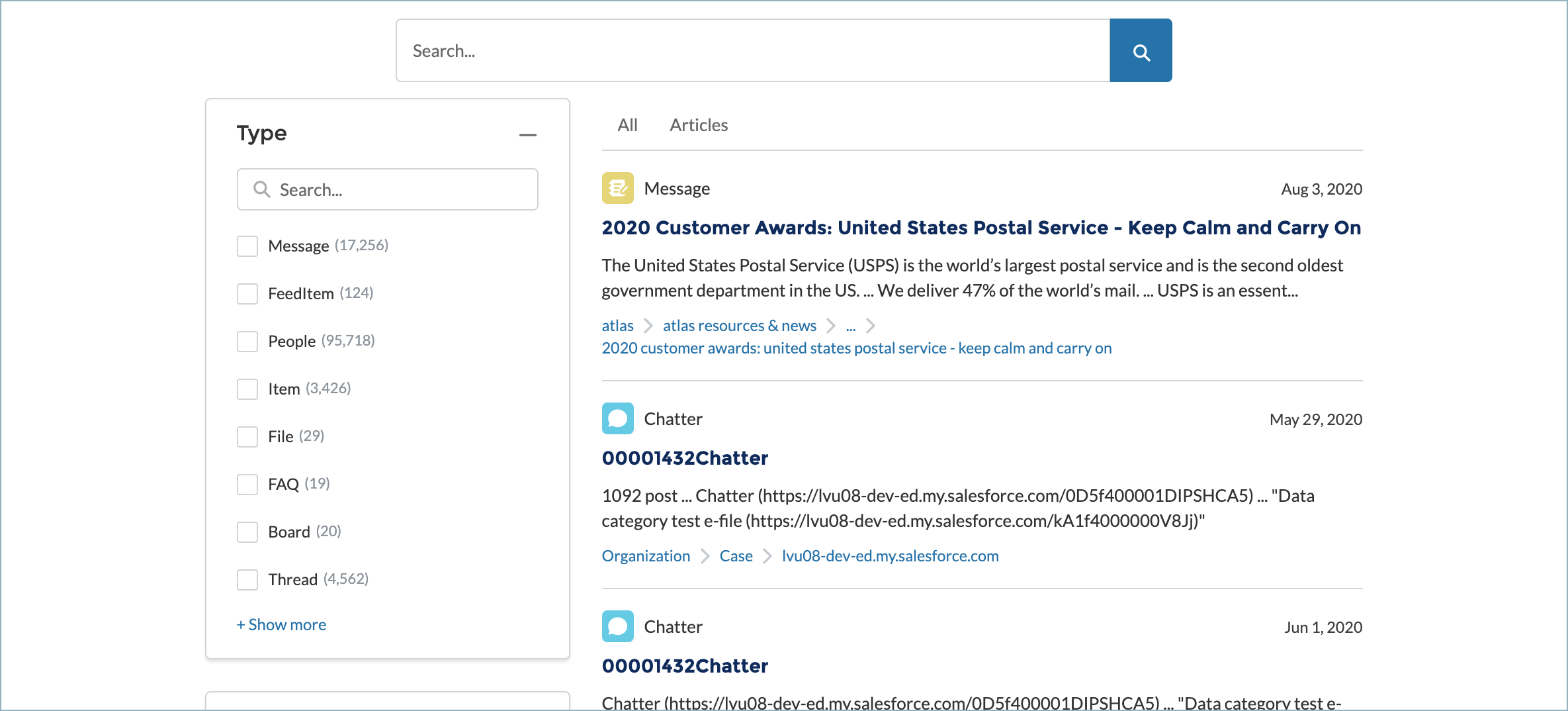
However, these results come from a sample organization which is only meant for testing. For a real implementation, you need to configure search token authentication in your search page. This means that each user gets their own search token, with appropriate privileges to access your organization’s content. Personalized search tokens also let you use personalized usage analytics and machine learning features.
If you’ve installed and configured Coveo for Salesforce v4 or a later package in your Salesforce organization, it’s typically enough to copy the CoveoTokenProvider Apex class, along with its meta.xml file, into your Salesforce DX project.
This class can automatically fetch your Salesforce users' information to generate search tokens for them.
This is the best option for most use cases.
If you haven’t installed Coveo for Salesforce v4 or a later package, or if the CoveoTokenProvider Apex class doesn’t fit your needs, you’ll have to implement your own search token provider.
|
|
You can find an example in the Quantic project repository. |
Once you’ve copied or created your search token provider Apex class, you need to modify the Headless configuration in your Quantic installation so that it calls your Apex class.
You can find the HeadlessController file at force-app/quantic/classes.
Locate the following line:
return SampleTokenProvider.getHeadlessConfiguration();and modify it so that it leverages your search token provider instead:
return YOUR_TOKEN_PROVIDER.getHeadlessConfiguration();where you replace YOUR_TOKEN_PROVIDER with the name of your search token provider Apex class, such as CoveoTokenProvider if you copied it from the Quantic project.
If you’ve retrieved the Quantic project, you can make this change locally.
After you deploy your project, your changes will be effective in your Salesforce organization.
If you haven’t retrieved Quantic locally, you can navigate to the HeadlessController file from the Salesforce Developer Console and modify it there.
Deploy your project
Deploy your project to your Salesforce organization with the project deploy start command:
sf project deploy start --target-org <YOUR_USERNAME>|
|
If you get an error message, you may need to rename some files. For example, you may need to rename the following file:
to
|
After you’ve deployed your project successfully, you’ll be able to use your LWC in the Salesforce Experience Builder.
Update Quantic
The process for updating the Quantic project is similar to that for other Salesforce packages.
-
Start by installing the latest version.
-
If you retrieved the Quantic project locally in your Salesforce DX project, you’ll need to do so again to keep your project version in sync with the new one in your Salesforce organization.
-
The search token provider in the
HeadlessControllerfile gets overwritten by updates. You have to replaceSampleTokenProviderwith the name of your search token provider Apex class, as you did when you configured your search token provider.
What’s next?
After you implement a main search page in an Experience Cloud site (such as Community), you’ll typically want to implement a standalone search box.